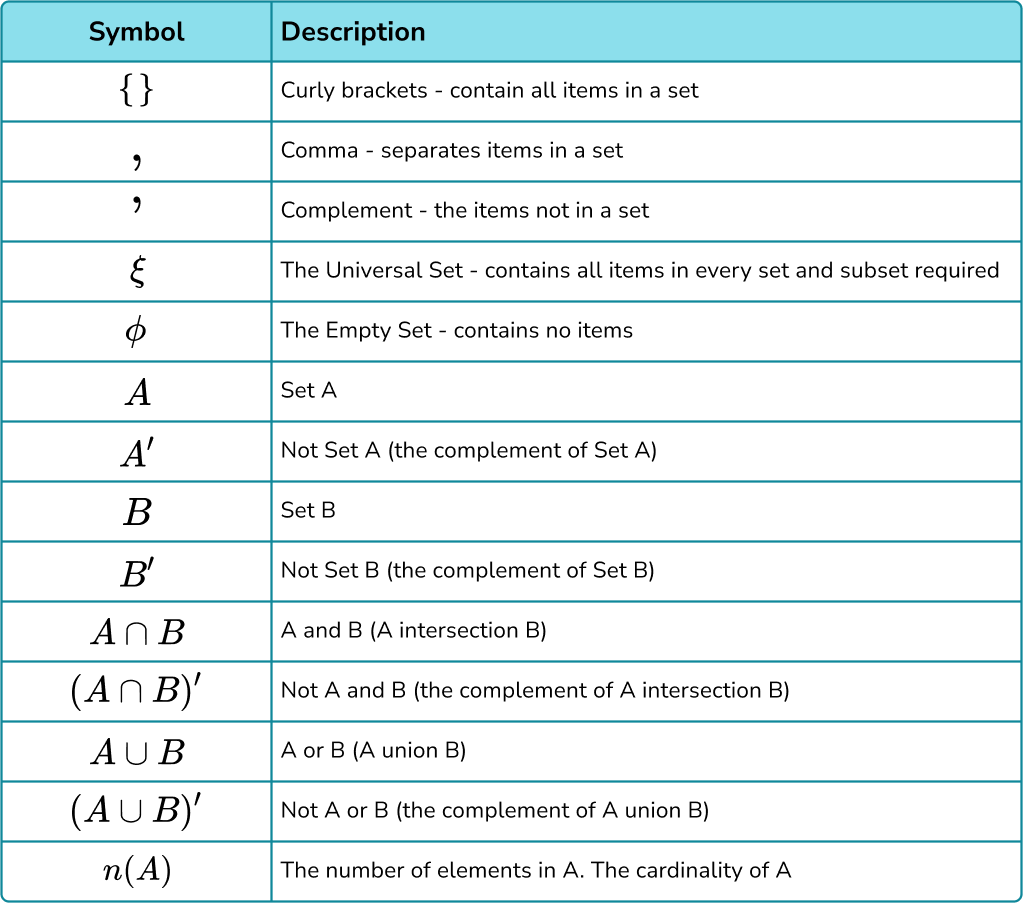
Set Notation Discrete Math
Set Notation Discrete Math - A set is a collection of things, usually numbers. This is read, “ a is the set containing the elements 1, 2 and 3.”. We need some notation to make talking about sets easier. For example, the set of natural numbers is defined as \[\mathbb{n} =. Consider, a = {1, 2, 3}. In that context the set $s$ is considered to be an alphabet and $s^*$ just. We can list each element (or member) of a set inside curly brackets. We take the pythonic approach that assumes that starting with zero is more natural than starting at one. For example, the set of natural numbers is defined as \[\mathbb{n} =. This notation is most common in discrete mathematics.
Consider, a = {1, 2, 3}. We take the pythonic approach that assumes that starting with zero is more natural than starting at one. This is read, “ a is the set containing the elements 1, 2 and 3.”. This notation is most common in discrete mathematics. For example, the set of natural numbers is defined as \[\mathbb{n} =. A set is a collection of things, usually numbers. For example, the set of natural numbers is defined as \[\mathbb{n} =. We can list each element (or member) of a set inside curly brackets. We need some notation to make talking about sets easier. In that context the set $s$ is considered to be an alphabet and $s^*$ just.
We take the pythonic approach that assumes that starting with zero is more natural than starting at one. Consider, a = {1, 2, 3}. This is read, “ a is the set containing the elements 1, 2 and 3.”. This notation is most common in discrete mathematics. For example, the set of natural numbers is defined as \[\mathbb{n} =. In that context the set $s$ is considered to be an alphabet and $s^*$ just. A set is a collection of things, usually numbers. We need some notation to make talking about sets easier. We can list each element (or member) of a set inside curly brackets. For example, the set of natural numbers is defined as \[\mathbb{n} =.
Different Notations of Sets
For example, the set of natural numbers is defined as \[\mathbb{n} =. We take the pythonic approach that assumes that starting with zero is more natural than starting at one. In that context the set $s$ is considered to be an alphabet and $s^*$ just. A set is a collection of things, usually numbers. This is read, “ a is.
Set Notation GCSE Maths Steps, Examples & Worksheet
For example, the set of natural numbers is defined as \[\mathbb{n} =. We can list each element (or member) of a set inside curly brackets. For example, the set of natural numbers is defined as \[\mathbb{n} =. This is read, “ a is the set containing the elements 1, 2 and 3.”. We need some notation to make talking about.
Set Notation GCSE Maths Steps, Examples & Worksheet
A set is a collection of things, usually numbers. We need some notation to make talking about sets easier. Consider, a = {1, 2, 3}. In that context the set $s$ is considered to be an alphabet and $s^*$ just. We can list each element (or member) of a set inside curly brackets.
Set Notation Worksheet ⋆
For example, the set of natural numbers is defined as \[\mathbb{n} =. This notation is most common in discrete mathematics. In that context the set $s$ is considered to be an alphabet and $s^*$ just. We can list each element (or member) of a set inside curly brackets. A set is a collection of things, usually numbers.
Set Identities (Defined & Illustrated w/ 13+ Examples!)
For example, the set of natural numbers is defined as \[\mathbb{n} =. We need some notation to make talking about sets easier. We can list each element (or member) of a set inside curly brackets. A set is a collection of things, usually numbers. This is read, “ a is the set containing the elements 1, 2 and 3.”.
PPT Discrete Mathematics PowerPoint Presentation, free download ID
This notation is most common in discrete mathematics. For example, the set of natural numbers is defined as \[\mathbb{n} =. We need some notation to make talking about sets easier. For example, the set of natural numbers is defined as \[\mathbb{n} =. We can list each element (or member) of a set inside curly brackets.
PPT Discrete Mathematics Set Operations and Identities PowerPoint
This notation is most common in discrete mathematics. We can list each element (or member) of a set inside curly brackets. We need some notation to make talking about sets easier. This is read, “ a is the set containing the elements 1, 2 and 3.”. In that context the set $s$ is considered to be an alphabet and $s^*$.
How To Write In Set Builder Notation
This notation is most common in discrete mathematics. We take the pythonic approach that assumes that starting with zero is more natural than starting at one. A set is a collection of things, usually numbers. This is read, “ a is the set containing the elements 1, 2 and 3.”. Consider, a = {1, 2, 3}.
Discrete Mathematics 03 Set Theoretical Operations by Evangelos
This is read, “ a is the set containing the elements 1, 2 and 3.”. We can list each element (or member) of a set inside curly brackets. This notation is most common in discrete mathematics. A set is a collection of things, usually numbers. For example, the set of natural numbers is defined as \[\mathbb{n} =.
Discrete Math Tutorial Examples and Forms
For example, the set of natural numbers is defined as \[\mathbb{n} =. For example, the set of natural numbers is defined as \[\mathbb{n} =. Consider, a = {1, 2, 3}. We need some notation to make talking about sets easier. We can list each element (or member) of a set inside curly brackets.
In That Context The Set $S$ Is Considered To Be An Alphabet And $S^*$ Just.
For example, the set of natural numbers is defined as \[\mathbb{n} =. This notation is most common in discrete mathematics. A set is a collection of things, usually numbers. Consider, a = {1, 2, 3}.
For Example, The Set Of Natural Numbers Is Defined As \[\Mathbb{N} =.
We take the pythonic approach that assumes that starting with zero is more natural than starting at one. We can list each element (or member) of a set inside curly brackets. This is read, “ a is the set containing the elements 1, 2 and 3.”. We need some notation to make talking about sets easier.