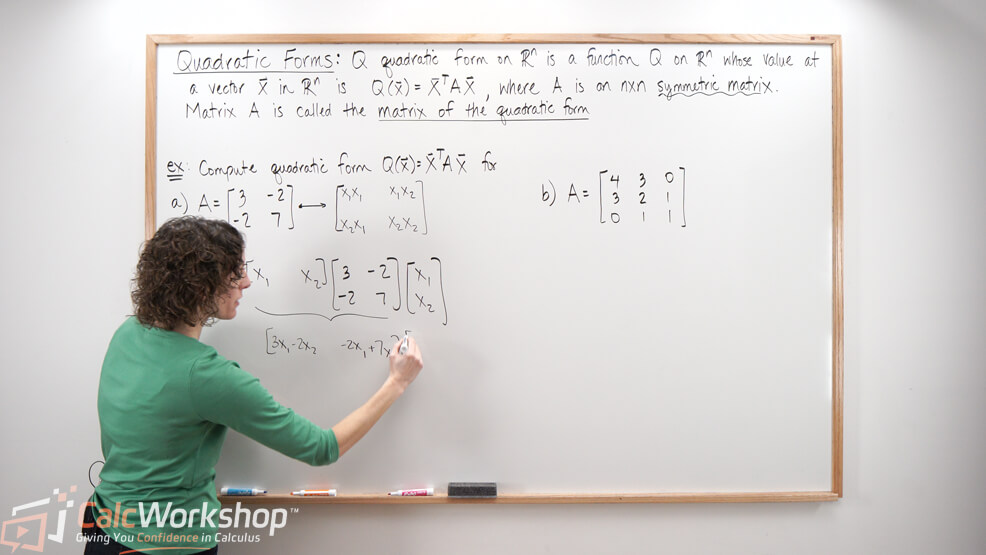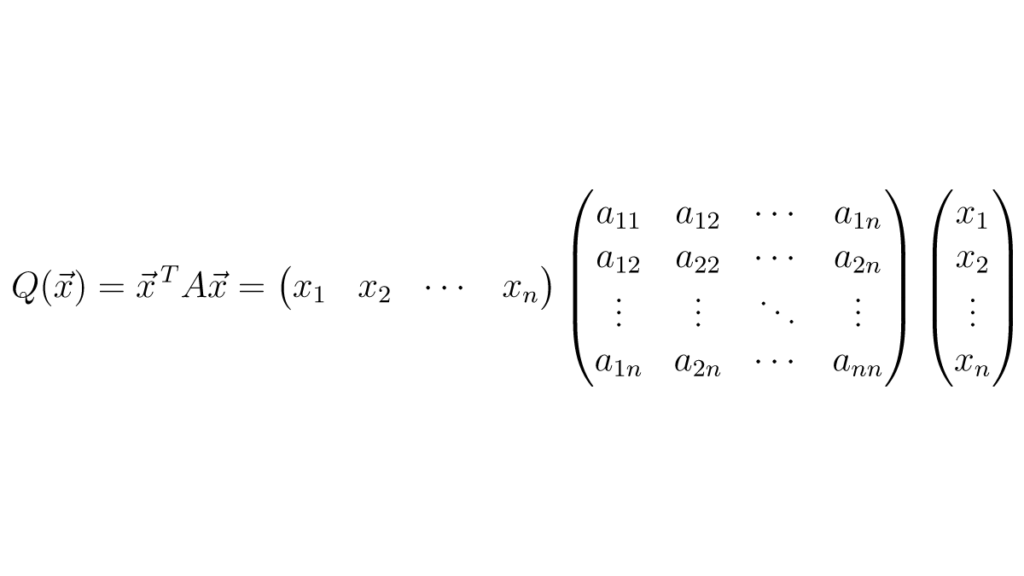Quadratic Form Matrix
Quadratic Form Matrix - The quadratic forms of a matrix comes up often in statistical applications. In this chapter, you will learn about the quadratic forms of a matrix. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. See examples of geometric interpretation, change of. Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no. The quadratic form q(x) involves a matrix a and a vector x. We can use this to define a quadratic form,. The matrix a is typically symmetric, meaning a t = a, and it determines. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix.
In this chapter, you will learn about the quadratic forms of a matrix. See examples of geometric interpretation, change of. Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. The quadratic form q(x) involves a matrix a and a vector x. The matrix a is typically symmetric, meaning a t = a, and it determines. We can use this to define a quadratic form,. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. The quadratic forms of a matrix comes up often in statistical applications.
See examples of geometric interpretation, change of. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no. The matrix a is typically symmetric, meaning a t = a, and it determines. The quadratic forms of a matrix comes up often in statistical applications. The quadratic form q(x) involves a matrix a and a vector x. In this chapter, you will learn about the quadratic forms of a matrix. We can use this to define a quadratic form,.
Quadratic Form (Matrix Approach for Conic Sections)
The matrix a is typically symmetric, meaning a t = a, and it determines. In this chapter, you will learn about the quadratic forms of a matrix. The quadratic form q(x) involves a matrix a and a vector x. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an.
9.1 matrix of a quad form
Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no. We can use this to define a quadratic form,. The quadratic form q(x) involves a matrix a and a vector x. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. See.
PPT Quadratic Forms, Characteristic Roots and Characteristic Vectors
Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no. Learn how to define, compute and interpret quadratic forms as functions.
Representing a Quadratic Form Using a Matrix Linear Combinations
See examples of geometric interpretation, change of. We can use this to define a quadratic form,. The quadratic form q(x) involves a matrix a and a vector x. The quadratic forms of a matrix comes up often in statistical applications. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices.
Quadratic Forms YouTube
Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. See examples of geometric interpretation, change of. We can use this to define a quadratic form,. The matrix a is typically.
Quadratic form Matrix form to Quadratic form Examples solved
We can use this to define a quadratic form,. In this chapter, you will learn about the quadratic forms of a matrix. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. The quadratic forms of a matrix comes up often in statistical applications. Recall that a bilinear form from r2m → r can be written.
SOLVEDExpress the quadratic equation in the matr…
In this chapter, you will learn about the quadratic forms of a matrix. The matrix a is typically symmetric, meaning a t = a, and it determines. We can use this to define a quadratic form,. The quadratic form q(x) involves a matrix a and a vector x. Learn how to define, compute and interpret quadratic forms as functions of.
Linear Algebra Quadratic Forms YouTube
The matrix a is typically symmetric, meaning a t = a, and it determines. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. We can use this to define a quadratic form,. In this chapter, you will learn about the quadratic forms of a.
Solved (1 point) Write the matrix of the quadratic form Q(x,
In this chapter, you will learn about the quadratic forms of a matrix. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no. Recall that a bilinear form from r2m → r.
Definiteness of Hermitian Matrices Part 1/4 "Quadratic Forms" YouTube
Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. The matrix a is typically symmetric, meaning a t = a, and it determines. In this chapter, you will learn about the quadratic forms of a matrix. The quadratic form q(x) involves a matrix a.
The Quadratic Form Q(X) Involves A Matrix A And A Vector X.
The quadratic forms of a matrix comes up often in statistical applications. See examples of geometric interpretation, change of. In this chapter, you will learn about the quadratic forms of a matrix. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix.
Learn How To Define, Compute And Interpret Quadratic Forms As Functions Of Symmetric Matrices.
The matrix a is typically symmetric, meaning a t = a, and it determines. We can use this to define a quadratic form,. Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no.