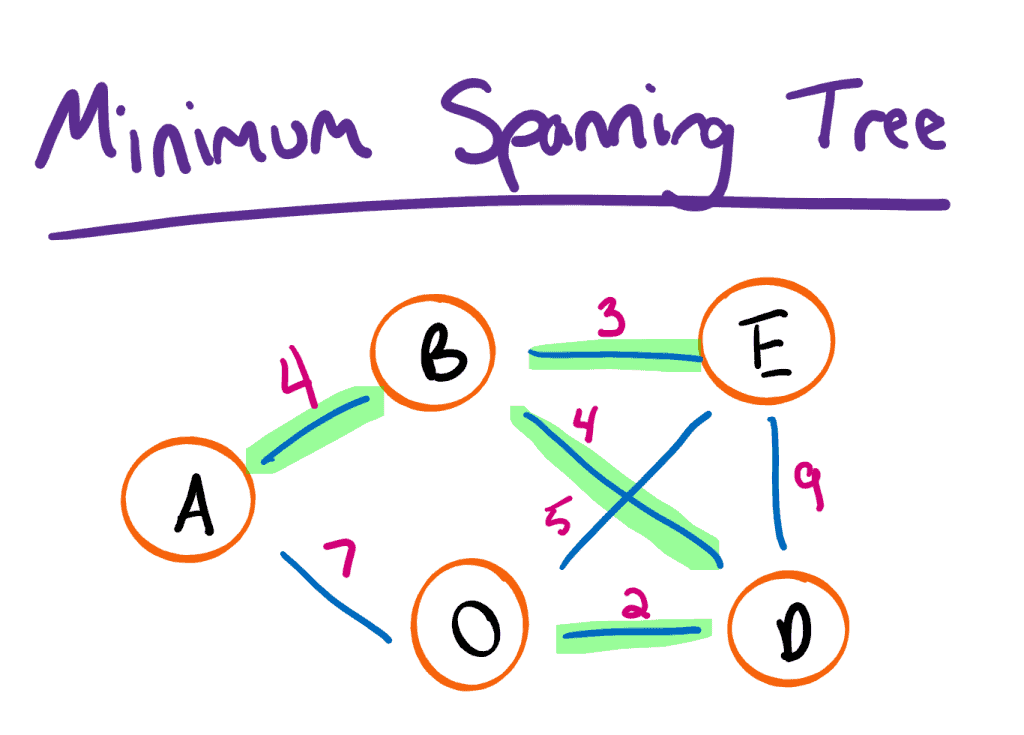
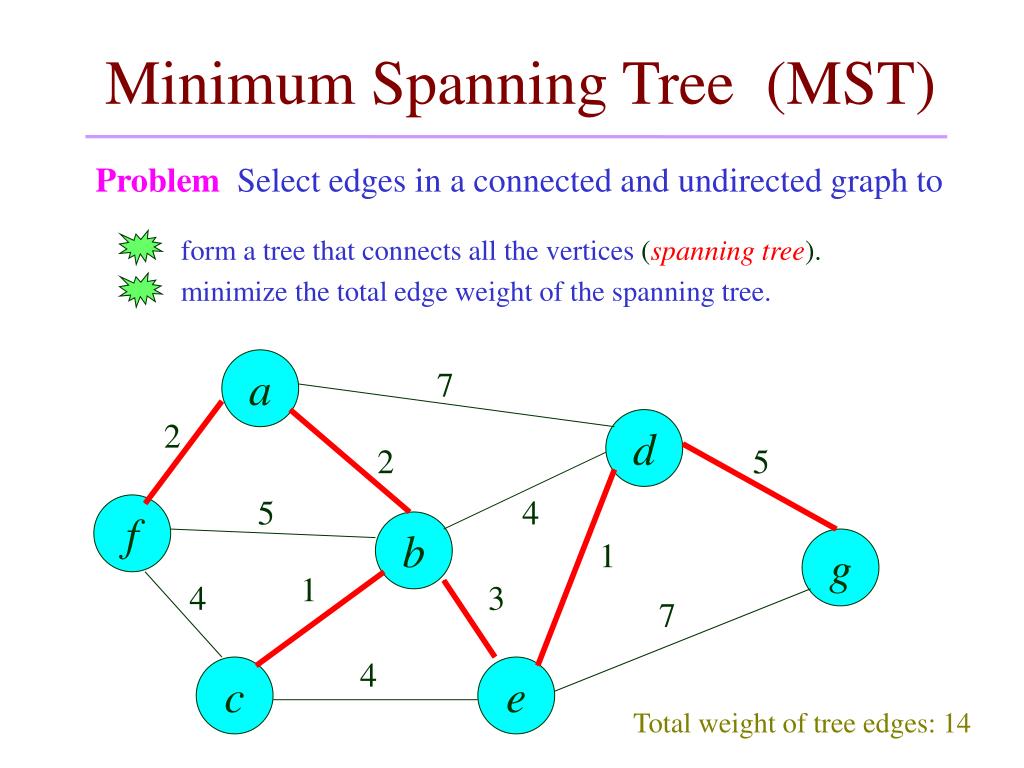
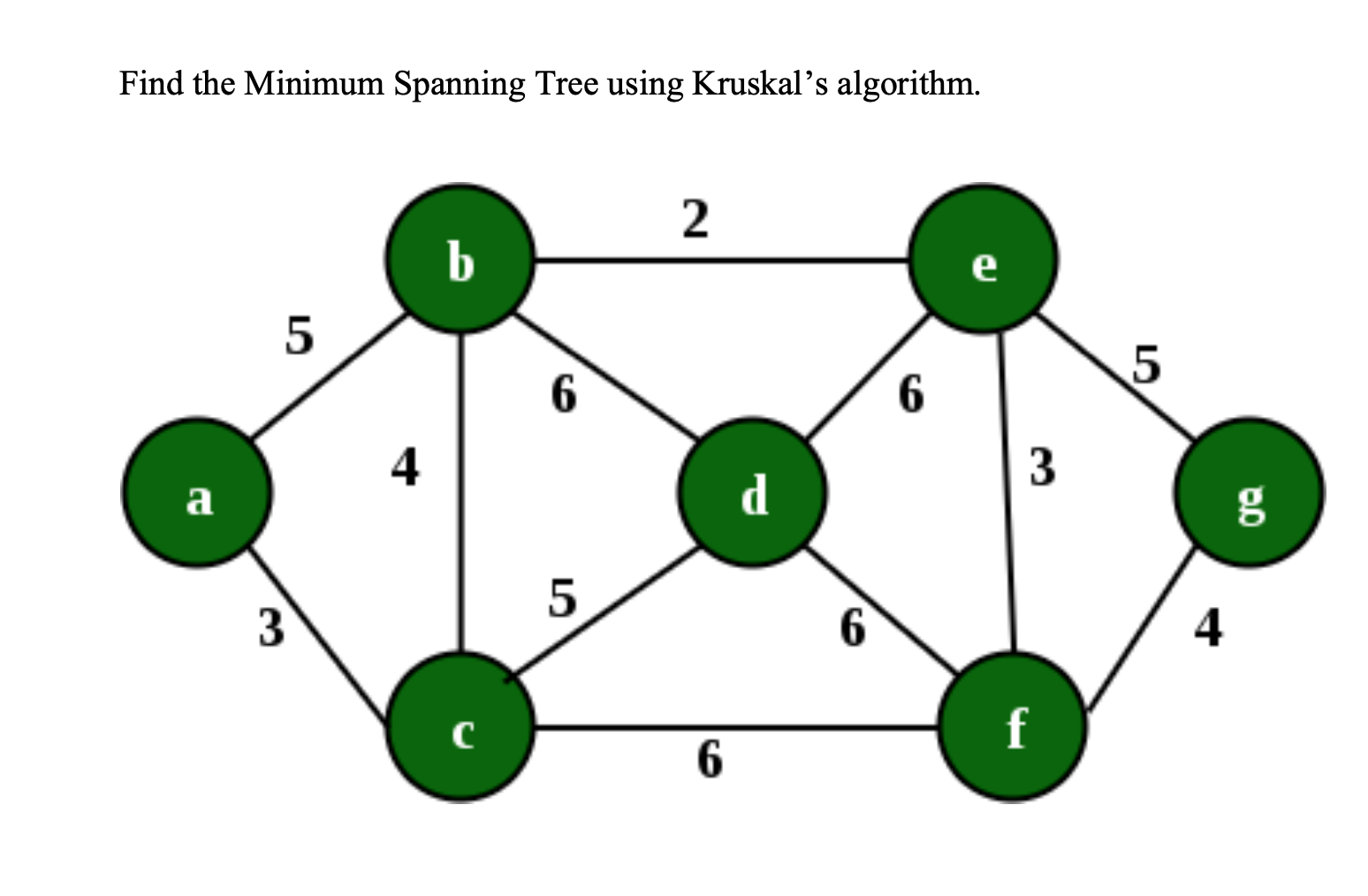
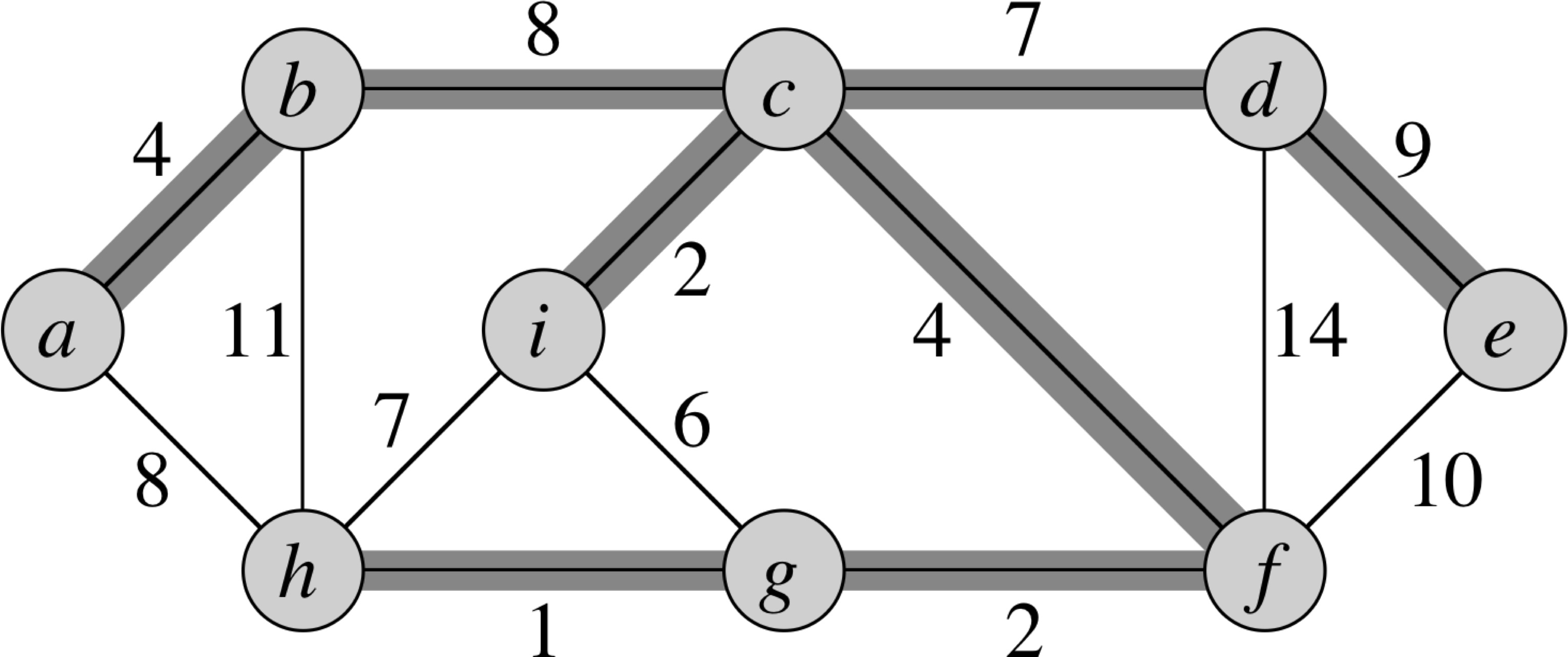
Minimum Spanning Tree
Minimum Spanning Tree - (proving that this works is tedious but doable.) this would give an algorithm of cost o(t(m, n) + kn), since you would be building. Add {u, v} to the spanning tree. I think the best way of finding the number of minimum spanning tree must be something. There is only one minimum spanning tree in the graph where the weights of vertices are different. As far as i can tell, removal requires o(n^2), because for each edge (assume sorted already in a list), we need to find the smallest edge which connects the two spanning trees. The fastest minimum spanning tree algorithm to date was developed by david karger, philip klein, and robert tarjan, who found a linear time randomized algorithm based on a combination of. Return the resulting tree t'. It should be a spanning tree, since if a network isn’t a tree you can always remove some edges and save money.
Add {u, v} to the spanning tree. The fastest minimum spanning tree algorithm to date was developed by david karger, philip klein, and robert tarjan, who found a linear time randomized algorithm based on a combination of. It should be a spanning tree, since if a network isn’t a tree you can always remove some edges and save money. (proving that this works is tedious but doable.) this would give an algorithm of cost o(t(m, n) + kn), since you would be building. Return the resulting tree t'. As far as i can tell, removal requires o(n^2), because for each edge (assume sorted already in a list), we need to find the smallest edge which connects the two spanning trees. I think the best way of finding the number of minimum spanning tree must be something. There is only one minimum spanning tree in the graph where the weights of vertices are different.
It should be a spanning tree, since if a network isn’t a tree you can always remove some edges and save money. I think the best way of finding the number of minimum spanning tree must be something. There is only one minimum spanning tree in the graph where the weights of vertices are different. The fastest minimum spanning tree algorithm to date was developed by david karger, philip klein, and robert tarjan, who found a linear time randomized algorithm based on a combination of. Add {u, v} to the spanning tree. Return the resulting tree t'. (proving that this works is tedious but doable.) this would give an algorithm of cost o(t(m, n) + kn), since you would be building. As far as i can tell, removal requires o(n^2), because for each edge (assume sorted already in a list), we need to find the smallest edge which connects the two spanning trees.
Graphs Finding Minimum Spanning Trees with Kruskal's Algorithm a
It should be a spanning tree, since if a network isn’t a tree you can always remove some edges and save money. (proving that this works is tedious but doable.) this would give an algorithm of cost o(t(m, n) + kn), since you would be building. There is only one minimum spanning tree in the graph where the weights of.
Minimum Spanning Tree Algorithms The Renegade Coder
(proving that this works is tedious but doable.) this would give an algorithm of cost o(t(m, n) + kn), since you would be building. There is only one minimum spanning tree in the graph where the weights of vertices are different. The fastest minimum spanning tree algorithm to date was developed by david karger, philip klein, and robert tarjan, who.
PPT Minimum Spanning Tree (MST) PowerPoint Presentation, free
I think the best way of finding the number of minimum spanning tree must be something. Return the resulting tree t'. There is only one minimum spanning tree in the graph where the weights of vertices are different. It should be a spanning tree, since if a network isn’t a tree you can always remove some edges and save money..
Answered Find the Minimum Spanning Tree using… bartleby
There is only one minimum spanning tree in the graph where the weights of vertices are different. As far as i can tell, removal requires o(n^2), because for each edge (assume sorted already in a list), we need to find the smallest edge which connects the two spanning trees. It should be a spanning tree, since if a network isn’t.
Minimum Spanning Tree
As far as i can tell, removal requires o(n^2), because for each edge (assume sorted already in a list), we need to find the smallest edge which connects the two spanning trees. Return the resulting tree t'. I think the best way of finding the number of minimum spanning tree must be something. There is only one minimum spanning tree.
Minimum spanning tree C Data Structures and Algorithms
It should be a spanning tree, since if a network isn’t a tree you can always remove some edges and save money. There is only one minimum spanning tree in the graph where the weights of vertices are different. As far as i can tell, removal requires o(n^2), because for each edge (assume sorted already in a list), we need.
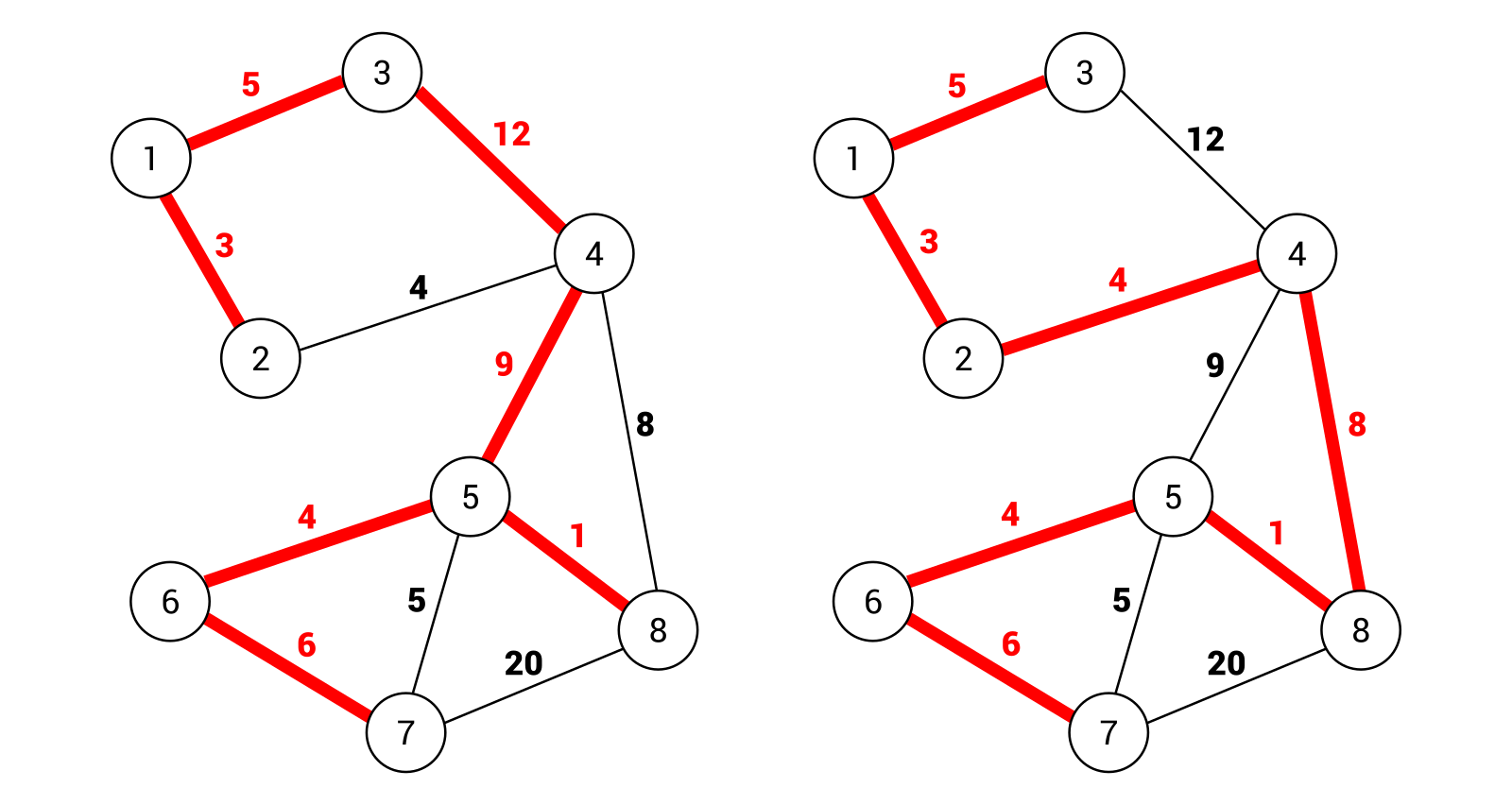
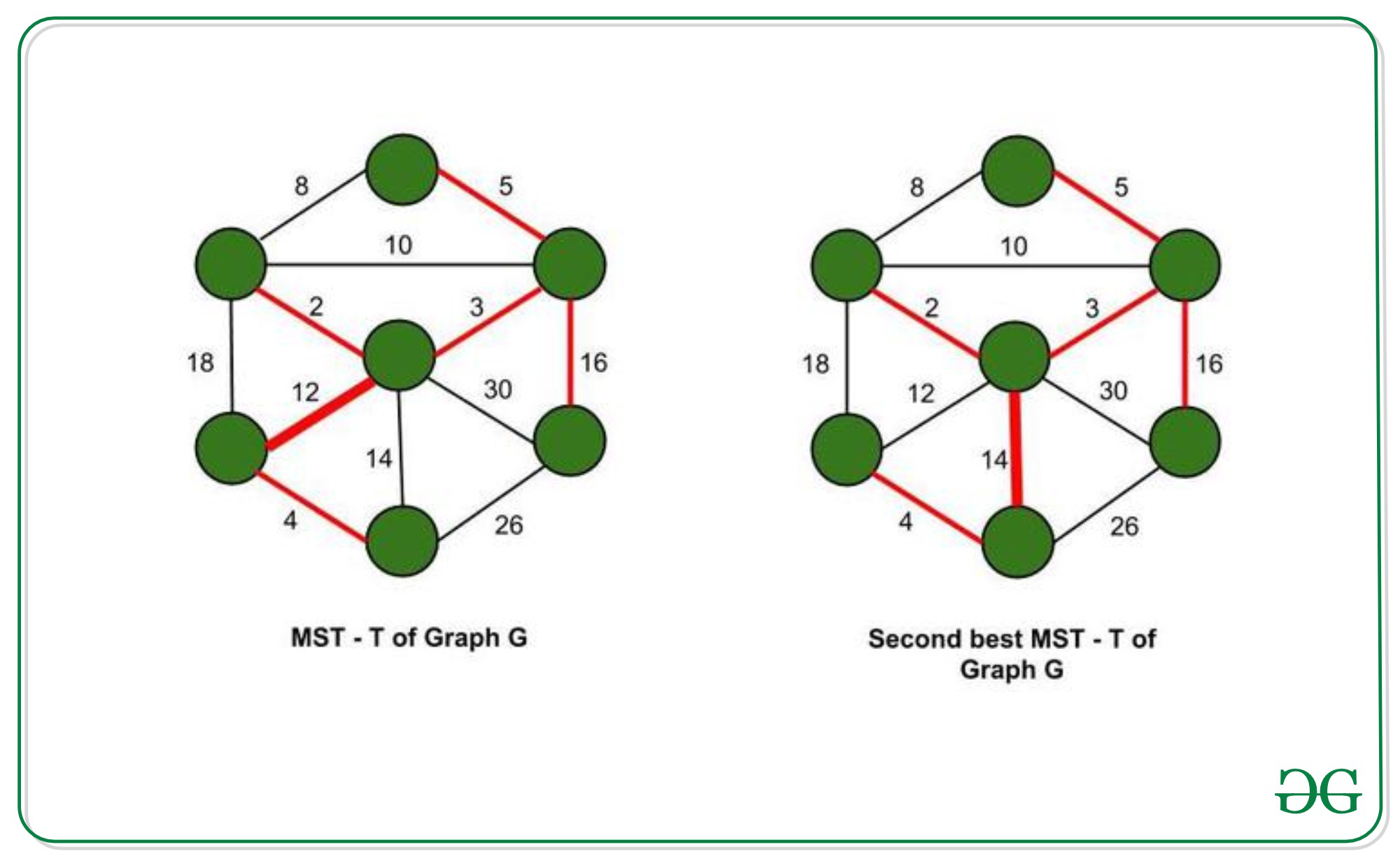
Second Best Minimum Spanning Tree
(proving that this works is tedious but doable.) this would give an algorithm of cost o(t(m, n) + kn), since you would be building. As far as i can tell, removal requires o(n^2), because for each edge (assume sorted already in a list), we need to find the smallest edge which connects the two spanning trees. I think the best.
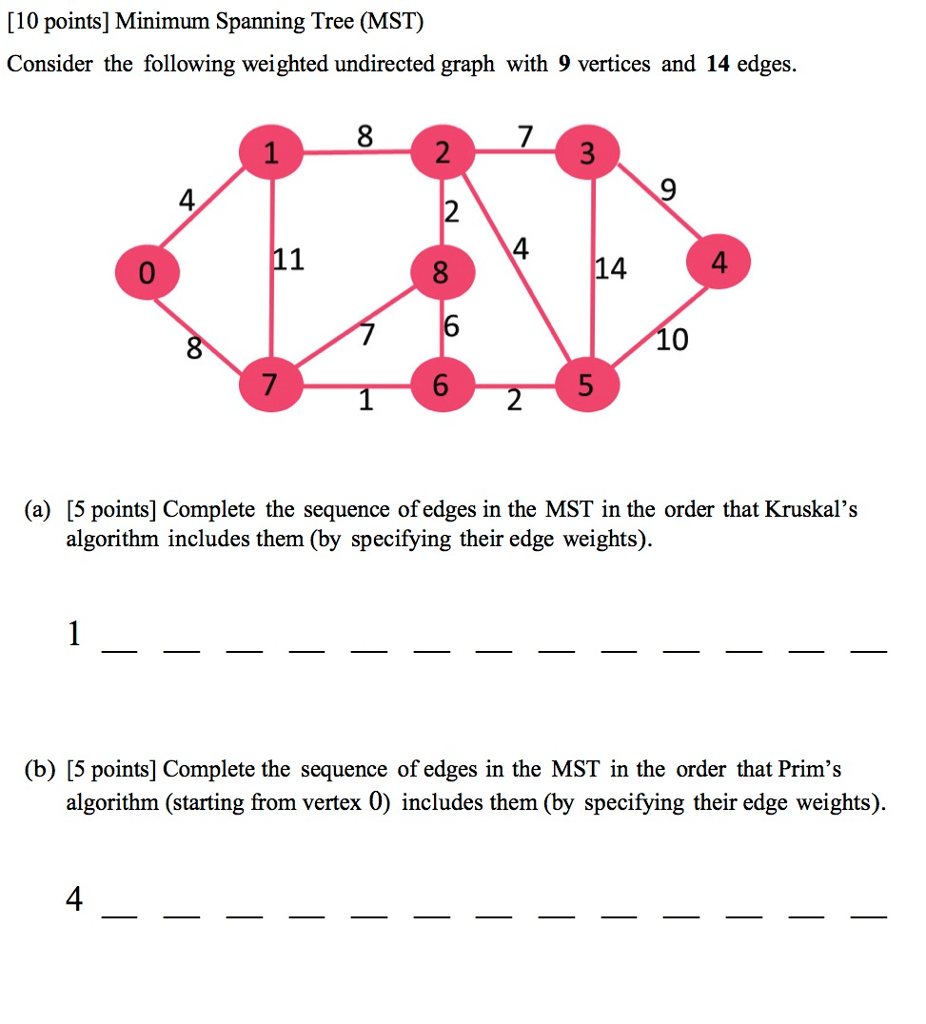
Solved Minimum Spanning Tree (MST) Consider the following
As far as i can tell, removal requires o(n^2), because for each edge (assume sorted already in a list), we need to find the smallest edge which connects the two spanning trees. The fastest minimum spanning tree algorithm to date was developed by david karger, philip klein, and robert tarjan, who found a linear time randomized algorithm based on a.
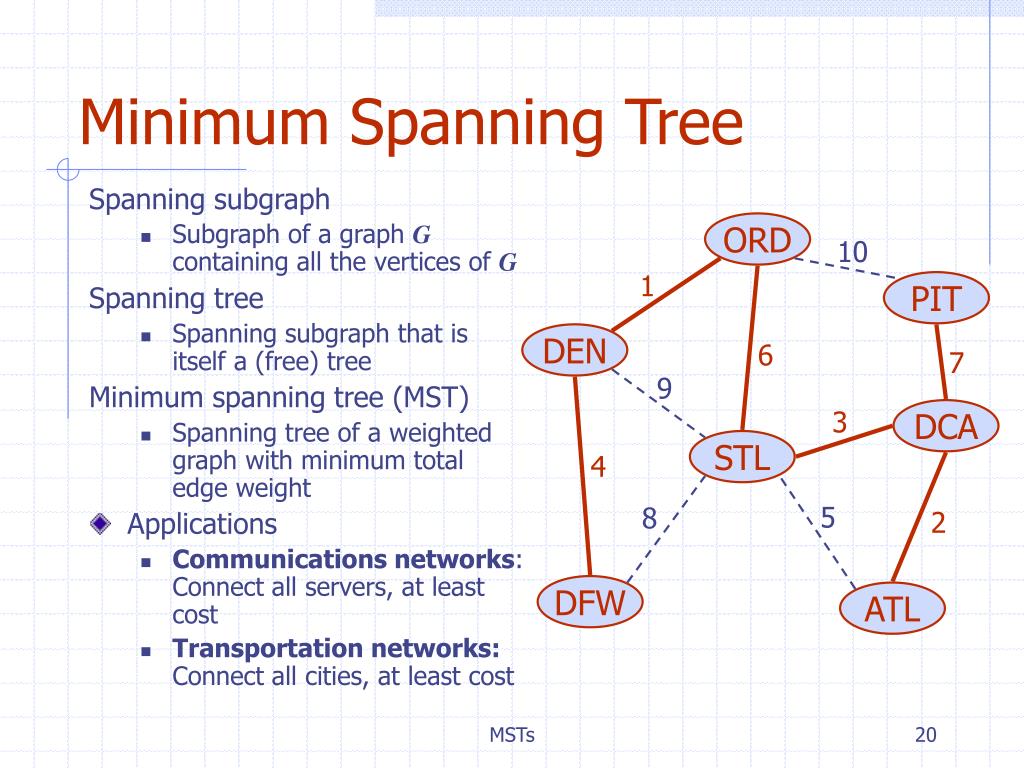
Data Structure Minimum Spanning Tree
Add {u, v} to the spanning tree. There is only one minimum spanning tree in the graph where the weights of vertices are different. (proving that this works is tedious but doable.) this would give an algorithm of cost o(t(m, n) + kn), since you would be building. Return the resulting tree t'. I think the best way of finding.
Minimum Spanning Tree Definition Examples Prim S Algorithm Riset
(proving that this works is tedious but doable.) this would give an algorithm of cost o(t(m, n) + kn), since you would be building. It should be a spanning tree, since if a network isn’t a tree you can always remove some edges and save money. As far as i can tell, removal requires o(n^2), because for each edge (assume.
Return The Resulting Tree T'.
(proving that this works is tedious but doable.) this would give an algorithm of cost o(t(m, n) + kn), since you would be building. There is only one minimum spanning tree in the graph where the weights of vertices are different. The fastest minimum spanning tree algorithm to date was developed by david karger, philip klein, and robert tarjan, who found a linear time randomized algorithm based on a combination of. As far as i can tell, removal requires o(n^2), because for each edge (assume sorted already in a list), we need to find the smallest edge which connects the two spanning trees.
It Should Be A Spanning Tree, Since If A Network Isn’t A Tree You Can Always Remove Some Edges And Save Money.
I think the best way of finding the number of minimum spanning tree must be something. Add {u, v} to the spanning tree.