Image Definition Math
Image Definition Math - In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs that can be obtained. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it.
In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs that can be obtained. In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\).
In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs that can be obtained. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it.
Math Mean Definition
In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs.
"Nabla Operator Definition Math And Calculus Basics" Poster for Sale
The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs.
Whole Numbers Definition and Examples in Math in 2022 Number
In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs that can be obtained. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is.
Identity Property in Math Definition and Examples
The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs.
DefinitionMath PropertiesIdentity Element for Multiplication
In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs that can be obtained. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is.
Solution Math Definition Example
In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs that can be obtained. In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is.
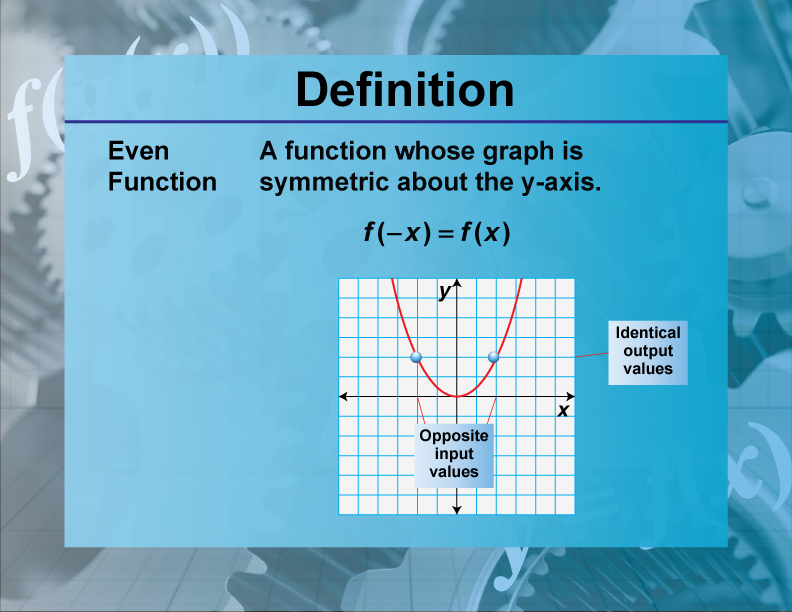
Function Math Definition
In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs.
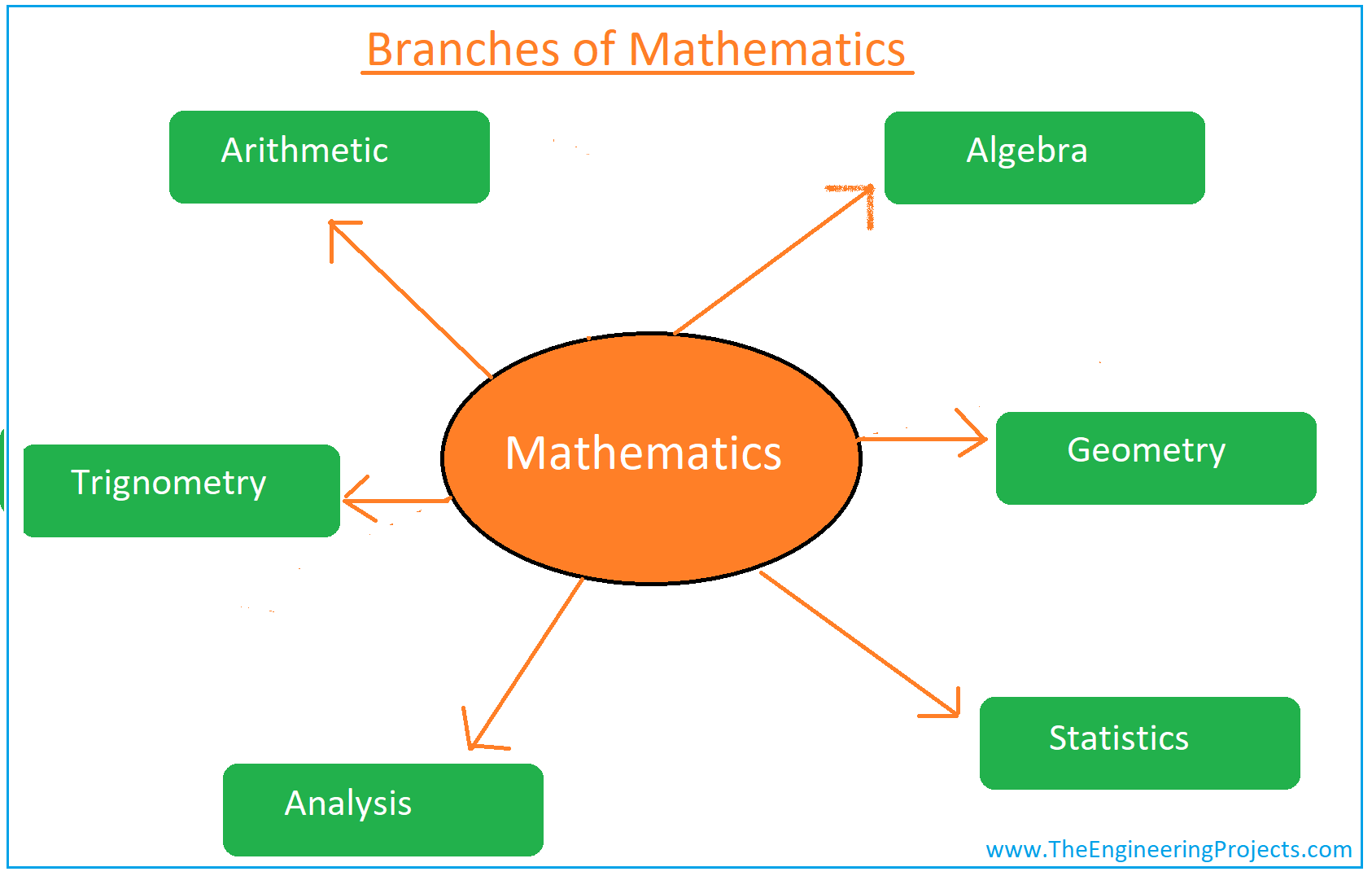
ज्ञानगंगोत्री MATHS
In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs.
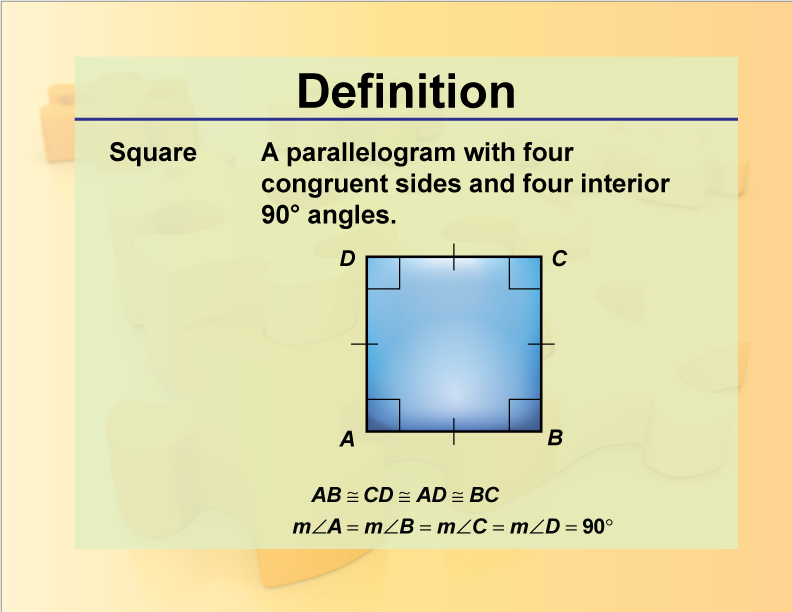
DefinitionGeometry BasicsSquare Media4Math
In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs.
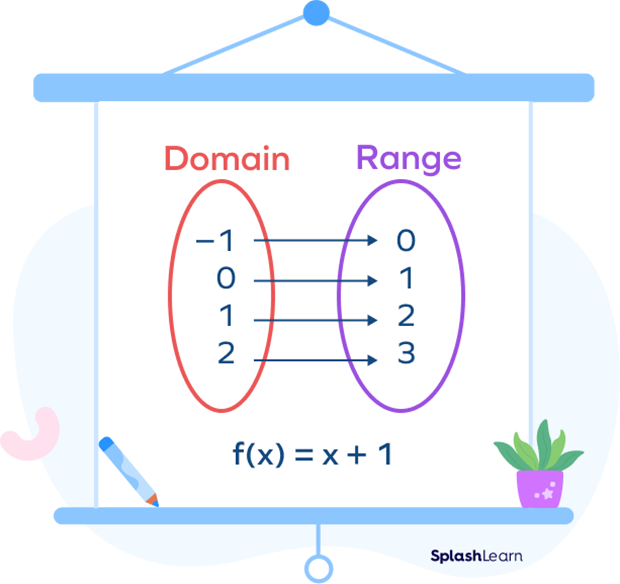
Range Math Definition
In mathematics, particularly in the context of functions, the image of a set is the collection of all outputs that can be obtained. The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set.
In Mathematics, Particularly In The Context Of Functions, The Image Of A Set Is The Collection Of All Outputs That Can Be Obtained.
The image of \(a_{1}\) under \(f\) is \[f\left(a_{1}\right)=\left\{f(a) \mid a \in a_{1}\right\}.\] it is a subset of \(b\). In mathematics, particularly in the study of algebraic structures and homomorphisms, the image of a function is the set of all outputs it.