Discrete Math Recurrence Relations
Discrete Math Recurrence Relations - Characteristic equation of recurrence relation i the recurrence relations have solutions of the form a n = rn, where r is a constant. Lucky for us, there are a few techniques for converting recursive definitions to closed formulas. Our primary focus will be on the class of finite order linear recurrence relations with constant coefficients (shortened to finite order. Doing so is called solving a recurrence relation.
Lucky for us, there are a few techniques for converting recursive definitions to closed formulas. Doing so is called solving a recurrence relation. Our primary focus will be on the class of finite order linear recurrence relations with constant coefficients (shortened to finite order. Characteristic equation of recurrence relation i the recurrence relations have solutions of the form a n = rn, where r is a constant.
Our primary focus will be on the class of finite order linear recurrence relations with constant coefficients (shortened to finite order. Characteristic equation of recurrence relation i the recurrence relations have solutions of the form a n = rn, where r is a constant. Doing so is called solving a recurrence relation. Lucky for us, there are a few techniques for converting recursive definitions to closed formulas.
Recurrence Relation GCSE Maths Steps And Examples
Characteristic equation of recurrence relation i the recurrence relations have solutions of the form a n = rn, where r is a constant. Our primary focus will be on the class of finite order linear recurrence relations with constant coefficients (shortened to finite order. Lucky for us, there are a few techniques for converting recursive definitions to closed formulas. Doing.
Solved DISCRETE MATH RECURRENCE RELATION
Doing so is called solving a recurrence relation. Our primary focus will be on the class of finite order linear recurrence relations with constant coefficients (shortened to finite order. Characteristic equation of recurrence relation i the recurrence relations have solutions of the form a n = rn, where r is a constant. Lucky for us, there are a few techniques.
Discrete Math Relations
Lucky for us, there are a few techniques for converting recursive definitions to closed formulas. Characteristic equation of recurrence relation i the recurrence relations have solutions of the form a n = rn, where r is a constant. Our primary focus will be on the class of finite order linear recurrence relations with constant coefficients (shortened to finite order. Doing.
Discrete Math Recurrence Relations YouTube
Lucky for us, there are a few techniques for converting recursive definitions to closed formulas. Doing so is called solving a recurrence relation. Our primary focus will be on the class of finite order linear recurrence relations with constant coefficients (shortened to finite order. Characteristic equation of recurrence relation i the recurrence relations have solutions of the form a n.
Discrete Math 2.4.2 Recurrence Relations YouTube
Doing so is called solving a recurrence relation. Characteristic equation of recurrence relation i the recurrence relations have solutions of the form a n = rn, where r is a constant. Our primary focus will be on the class of finite order linear recurrence relations with constant coefficients (shortened to finite order. Lucky for us, there are a few techniques.
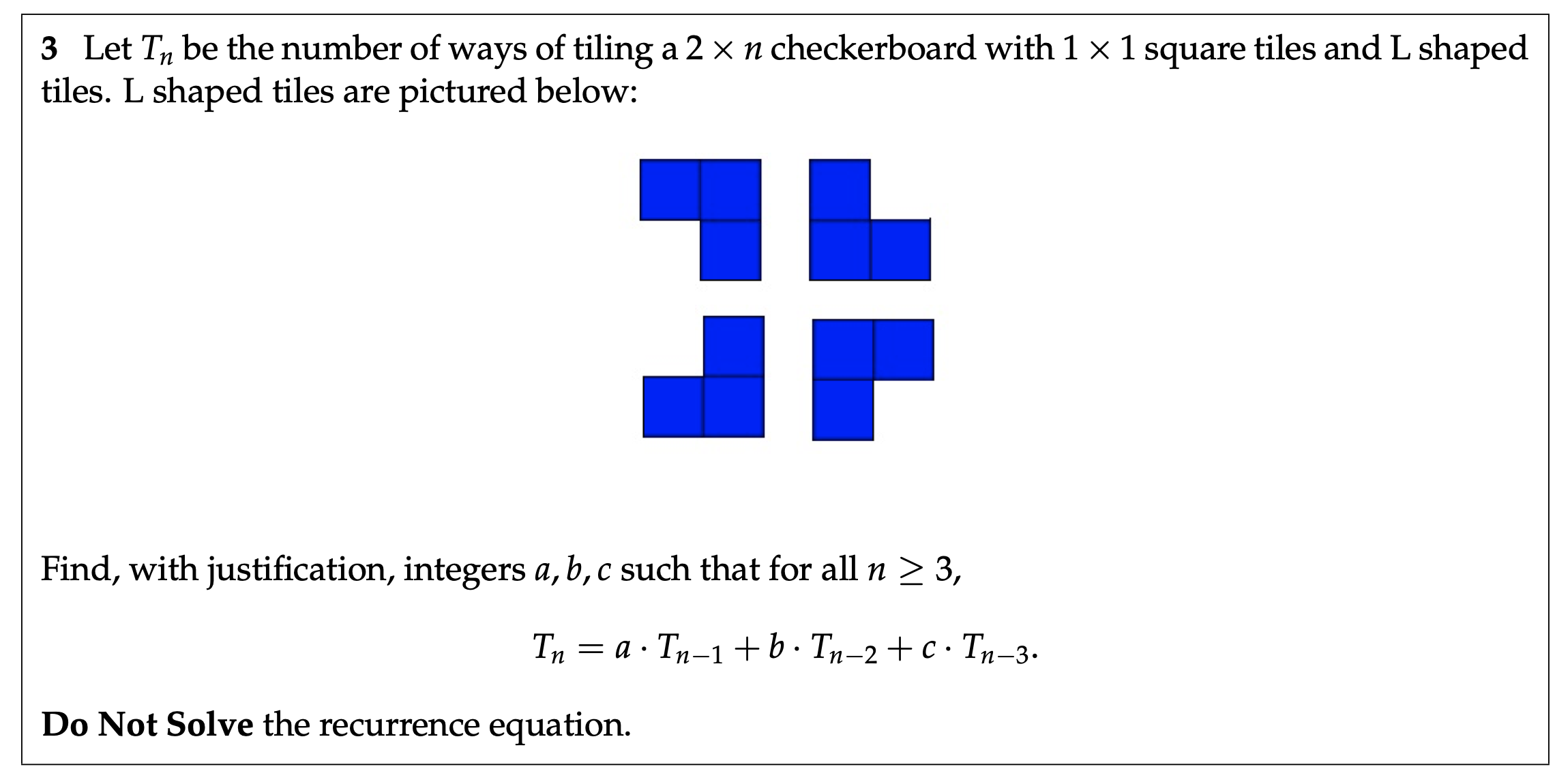
discrete math recurrence relations with tiles. Find
Lucky for us, there are a few techniques for converting recursive definitions to closed formulas. Characteristic equation of recurrence relation i the recurrence relations have solutions of the form a n = rn, where r is a constant. Our primary focus will be on the class of finite order linear recurrence relations with constant coefficients (shortened to finite order. Doing.
RECURRENCE RELATIONS using GENERATING FUNCTIONS DISCRETE MATHEMATICS
Characteristic equation of recurrence relation i the recurrence relations have solutions of the form a n = rn, where r is a constant. Our primary focus will be on the class of finite order linear recurrence relations with constant coefficients (shortened to finite order. Doing so is called solving a recurrence relation. Lucky for us, there are a few techniques.
Discrete Math 2 Tutorial 24 Linear Recurrence Relations YouTube
Our primary focus will be on the class of finite order linear recurrence relations with constant coefficients (shortened to finite order. Characteristic equation of recurrence relation i the recurrence relations have solutions of the form a n = rn, where r is a constant. Lucky for us, there are a few techniques for converting recursive definitions to closed formulas. Doing.
Discrete Math Recurrence Relations Codecademy
Characteristic equation of recurrence relation i the recurrence relations have solutions of the form a n = rn, where r is a constant. Doing so is called solving a recurrence relation. Our primary focus will be on the class of finite order linear recurrence relations with constant coefficients (shortened to finite order. Lucky for us, there are a few techniques.
Discrete Mathematics Lecture 3336 Recurrence Relations Math 3336
Doing so is called solving a recurrence relation. Our primary focus will be on the class of finite order linear recurrence relations with constant coefficients (shortened to finite order. Characteristic equation of recurrence relation i the recurrence relations have solutions of the form a n = rn, where r is a constant. Lucky for us, there are a few techniques.
Doing So Is Called Solving A Recurrence Relation.
Lucky for us, there are a few techniques for converting recursive definitions to closed formulas. Characteristic equation of recurrence relation i the recurrence relations have solutions of the form a n = rn, where r is a constant. Our primary focus will be on the class of finite order linear recurrence relations with constant coefficients (shortened to finite order.