Diagonalizable Matrix Khan Academy
Diagonalizable Matrix Khan Academy - This means that there exists an invertible matrix s such that b = s−1as is. Develop a library of examples of matrices that are and are not. We define a diagonal matrix. Learn two main criteria for a matrix to be diagonalizable. When a matrix is similar to a diagonal matrix, the matrix is said to be diagonalizable. Diagonalization of a matrix is defined as the process of reducing any matrix a into its diagonal form d. We say a matrix a is diagonalizable if it is similar to a diagonal matrix. Develop a library of examples of matrices that are and are not diagonalizable. Diagonalizability, when it occurs, gives you a good coordinate system to use for understanding a linear map (a set of axes built. Learn two main criteria for a matrix to be diagonalizable.
Diagonalization of a matrix is defined as the process of reducing any matrix a into its diagonal form d. When a matrix is similar to a diagonal matrix, the matrix is said to be diagonalizable. Develop a library of examples of matrices that are and are not. Diagonalizability, when it occurs, gives you a good coordinate system to use for understanding a linear map (a set of axes built. Develop a library of examples of matrices that are and are not diagonalizable. Learn two main criteria for a matrix to be diagonalizable. We define a diagonal matrix. Learn two main criteria for a matrix to be diagonalizable. We say a matrix a is diagonalizable if it is similar to a diagonal matrix. This means that there exists an invertible matrix s such that b = s−1as is.
Develop a library of examples of matrices that are and are not diagonalizable. This means that there exists an invertible matrix s such that b = s−1as is. Develop a library of examples of matrices that are and are not. Diagonalizability, when it occurs, gives you a good coordinate system to use for understanding a linear map (a set of axes built. Diagonalization of a matrix is defined as the process of reducing any matrix a into its diagonal form d. When a matrix is similar to a diagonal matrix, the matrix is said to be diagonalizable. Learn two main criteria for a matrix to be diagonalizable. Learn two main criteria for a matrix to be diagonalizable. We define a diagonal matrix. We say a matrix a is diagonalizable if it is similar to a diagonal matrix.
Solved Diagonalizable Matrices Definition An nxn matrix A
Learn two main criteria for a matrix to be diagonalizable. Diagonalization of a matrix is defined as the process of reducing any matrix a into its diagonal form d. This means that there exists an invertible matrix s such that b = s−1as is. We say a matrix a is diagonalizable if it is similar to a diagonal matrix. Diagonalizability,.
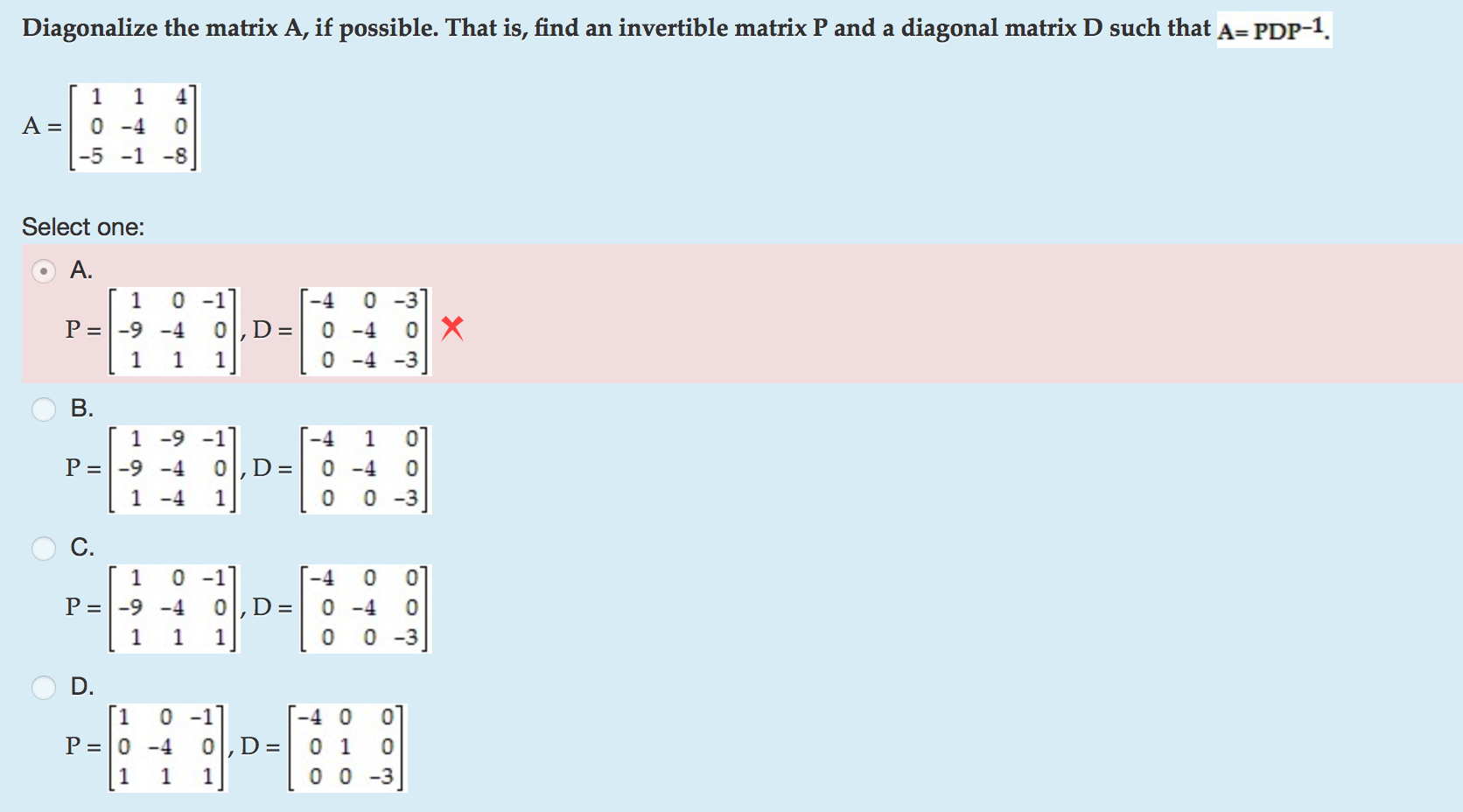
Solved Diagonalizable the matrix A, if possible. That is,
We define a diagonal matrix. Learn two main criteria for a matrix to be diagonalizable. Learn two main criteria for a matrix to be diagonalizable. Diagonalization of a matrix is defined as the process of reducing any matrix a into its diagonal form d. Develop a library of examples of matrices that are and are not.
Solved The matrix A is diagonalizable if A is similar to a
When a matrix is similar to a diagonal matrix, the matrix is said to be diagonalizable. Learn two main criteria for a matrix to be diagonalizable. Diagonalization of a matrix is defined as the process of reducing any matrix a into its diagonal form d. We say a matrix a is diagonalizable if it is similar to a diagonal matrix..
Khan AcademyMatrix Commercial YouTube
Develop a library of examples of matrices that are and are not diagonalizable. This means that there exists an invertible matrix s such that b = s−1as is. Develop a library of examples of matrices that are and are not. We define a diagonal matrix. Diagonalizability, when it occurs, gives you a good coordinate system to use for understanding a.
Diagonalizable Matrix University Example Diagonal & Transforming
This means that there exists an invertible matrix s such that b = s−1as is. Develop a library of examples of matrices that are and are not diagonalizable. Learn two main criteria for a matrix to be diagonalizable. When a matrix is similar to a diagonal matrix, the matrix is said to be diagonalizable. Develop a library of examples of.
Solved Orthogonal diagonalization A matrix A is
Diagonalizability, when it occurs, gives you a good coordinate system to use for understanding a linear map (a set of axes built. We say a matrix a is diagonalizable if it is similar to a diagonal matrix. Learn two main criteria for a matrix to be diagonalizable. Develop a library of examples of matrices that are and are not diagonalizable..
[Solved] . Prove that the symmetric matrix is diagonalizable. (Assume
This means that there exists an invertible matrix s such that b = s−1as is. We say a matrix a is diagonalizable if it is similar to a diagonal matrix. We define a diagonal matrix. Develop a library of examples of matrices that are and are not diagonalizable. Learn two main criteria for a matrix to be diagonalizable.
How to Diagonalize a Matrix StepbyStep Guide and Example
We say a matrix a is diagonalizable if it is similar to a diagonal matrix. Diagonalizability, when it occurs, gives you a good coordinate system to use for understanding a linear map (a set of axes built. We define a diagonal matrix. Learn two main criteria for a matrix to be diagonalizable. Learn two main criteria for a matrix to.
Solved If A is diagonalizable matrix of order n×n, then
Learn two main criteria for a matrix to be diagonalizable. Diagonalizability, when it occurs, gives you a good coordinate system to use for understanding a linear map (a set of axes built. Develop a library of examples of matrices that are and are not diagonalizable. We say a matrix a is diagonalizable if it is similar to a diagonal matrix..
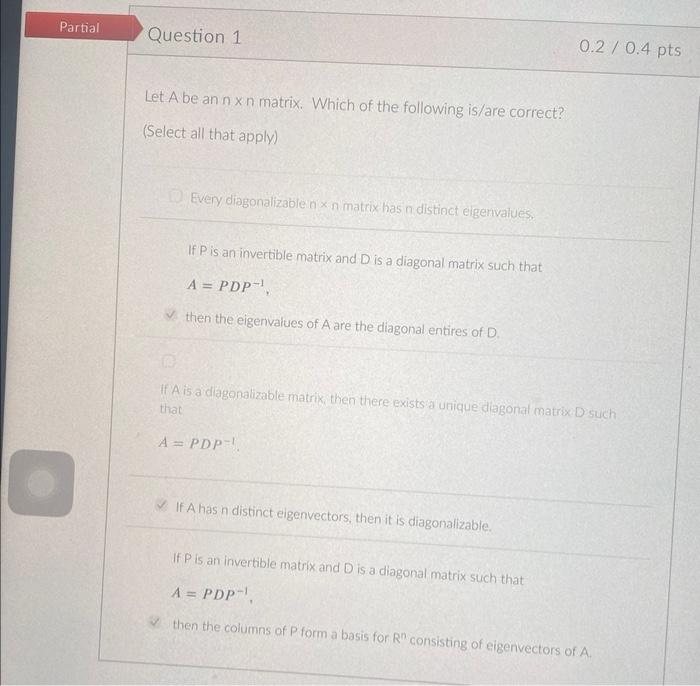
Solved Let A be an n×n matrix. Which of the following is/are
We define a diagonal matrix. Learn two main criteria for a matrix to be diagonalizable. We say a matrix a is diagonalizable if it is similar to a diagonal matrix. Learn two main criteria for a matrix to be diagonalizable. This means that there exists an invertible matrix s such that b = s−1as is.
Diagonalizability, When It Occurs, Gives You A Good Coordinate System To Use For Understanding A Linear Map (A Set Of Axes Built.
When a matrix is similar to a diagonal matrix, the matrix is said to be diagonalizable. We define a diagonal matrix. We say a matrix a is diagonalizable if it is similar to a diagonal matrix. Develop a library of examples of matrices that are and are not diagonalizable.
Learn Two Main Criteria For A Matrix To Be Diagonalizable.
Develop a library of examples of matrices that are and are not. Learn two main criteria for a matrix to be diagonalizable. This means that there exists an invertible matrix s such that b = s−1as is. Diagonalization of a matrix is defined as the process of reducing any matrix a into its diagonal form d.