Controllable Canonical Form
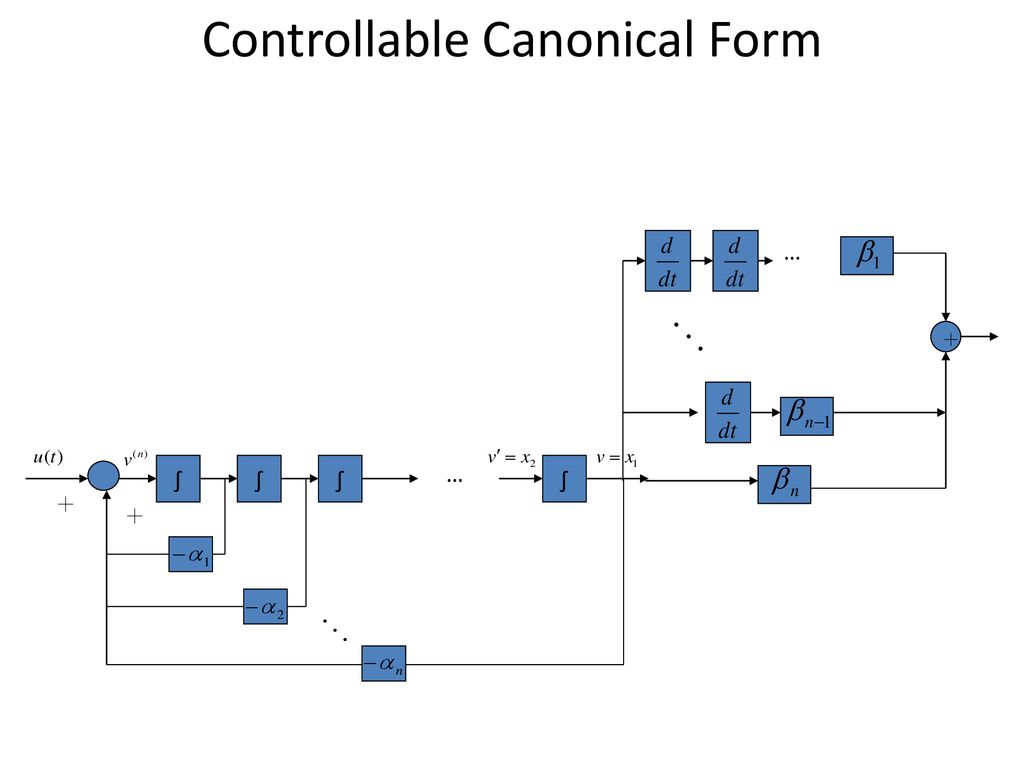
Controllable Canonical Form - This realization is called the controllable canonical form uw linear systems (x. Learn how to obtain controllable canonical form, a minimal realization of a system with the characteristic polynomial in the a matrix, using. We will see that there are multiple models (or realizations) that correspond to the same transfer function. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the.
Learn how to obtain controllable canonical form, a minimal realization of a system with the characteristic polynomial in the a matrix, using. We will see that there are multiple models (or realizations) that correspond to the same transfer function. This realization is called the controllable canonical form uw linear systems (x. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the.
Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the. This realization is called the controllable canonical form uw linear systems (x. Learn how to obtain controllable canonical form, a minimal realization of a system with the characteristic polynomial in the a matrix, using. We will see that there are multiple models (or realizations) that correspond to the same transfer function.
Feedback Control Systems (FCS) ppt download
Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the. We will see that there are multiple models (or realizations) that correspond to the same transfer function. This realization is called the controllable canonical form uw linear systems (x. Learn how to obtain controllable.
Controllable Canonical Phase Variable Form Method 1 Converting
We will see that there are multiple models (or realizations) that correspond to the same transfer function. Learn how to obtain controllable canonical form, a minimal realization of a system with the characteristic polynomial in the a matrix, using. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be.
Feedback Control Systems (FCS) ppt download
Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the. We will see that there are multiple models (or realizations) that correspond to the same transfer function. This realization is called the controllable canonical form uw linear systems (x. Learn how to obtain controllable.
Lecture 3 State Space Canonical forms YouTube
This realization is called the controllable canonical form uw linear systems (x. Learn how to obtain controllable canonical form, a minimal realization of a system with the characteristic polynomial in the a matrix, using. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the..
LCS 53a Controllable Canonical Form (CCF) statespace models YouTube
Learn how to obtain controllable canonical form, a minimal realization of a system with the characteristic polynomial in the a matrix, using. This realization is called the controllable canonical form uw linear systems (x. We will see that there are multiple models (or realizations) that correspond to the same transfer function. Theorem (kalman canonical form (controllability)) let x 2rn, x(k.
Feedback Control Systems (FCS) ppt download
Learn how to obtain controllable canonical form, a minimal realization of a system with the characteristic polynomial in the a matrix, using. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the. We will see that there are multiple models (or realizations) that correspond.
PPT Feedback Control Systems (FCS) PowerPoint Presentation, free
Learn how to obtain controllable canonical form, a minimal realization of a system with the characteristic polynomial in the a matrix, using. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the. We will see that there are multiple models (or realizations) that correspond.
controllable canonical form problem solving YouTube
Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the. We will see that there are multiple models (or realizations) that correspond to the same transfer function. Learn how to obtain controllable canonical form, a minimal realization of a system with the characteristic polynomial.
Easy Explanation of Controllable Canonical Form Control Engineering
This realization is called the controllable canonical form uw linear systems (x. Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the. We will see that there are multiple models (or realizations) that correspond to the same transfer function. Learn how to obtain controllable.
State Space Introduction Controllable Canonical Form YouTube
We will see that there are multiple models (or realizations) that correspond to the same transfer function. This realization is called the controllable canonical form uw linear systems (x. Learn how to obtain controllable canonical form, a minimal realization of a system with the characteristic polynomial in the a matrix, using. Theorem (kalman canonical form (controllability)) let x 2rn, x(k.
We Will See That There Are Multiple Models (Or Realizations) That Correspond To The Same Transfer Function.
Theorem (kalman canonical form (controllability)) let x 2rn, x(k + 1) = ax(k) + bu(k), y(k) = cx(k) + du(k) be uncontrollable with rank of the. This realization is called the controllable canonical form uw linear systems (x. Learn how to obtain controllable canonical form, a minimal realization of a system with the characteristic polynomial in the a matrix, using.
.jpg)

.jpg)