Conjugate Of A Complex Number In Polar Form

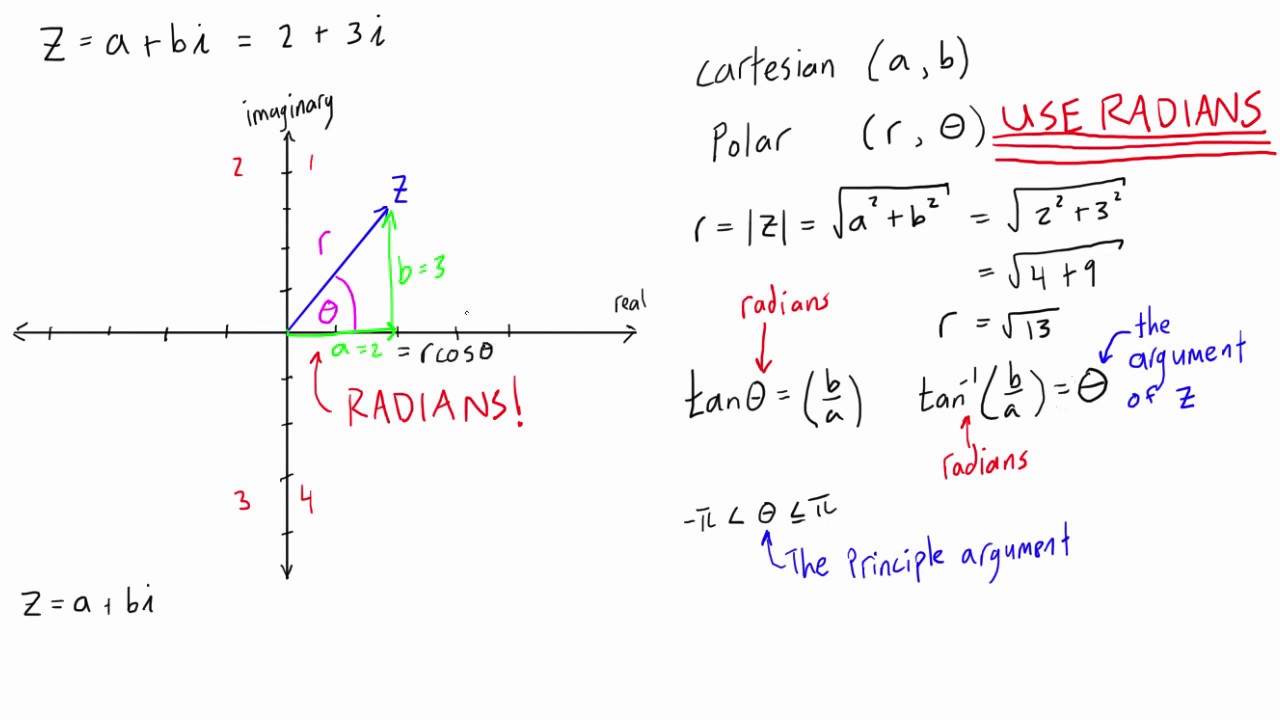
Conjugate Of A Complex Number In Polar Form - The conjugate of any purely. In polar coordinates complex conjugate of (r,θ) is (r, −θ). Finding the conjugate of a complex number in the polar form: What is the conjugate of the complex number (r, θ), in polar form? Let $z := r \paren {\cos \theta + i \sin \theta} \in \c$ be a complex number expressed in polar form. Let the complex number in the polar form with the coordinates (r, θ) is given by:

The conjugate of any purely. What is the conjugate of the complex number (r, θ), in polar form? In polar coordinates complex conjugate of (r,θ) is (r, −θ). Let $z := r \paren {\cos \theta + i \sin \theta} \in \c$ be a complex number expressed in polar form. Finding the conjugate of a complex number in the polar form: Let the complex number in the polar form with the coordinates (r, θ) is given by:

What is the conjugate of the complex number (r, θ), in polar form? The conjugate of any purely. Finding the conjugate of a complex number in the polar form: Let $z := r \paren {\cos \theta + i \sin \theta} \in \c$ be a complex number expressed in polar form. Let the complex number in the polar form with the coordinates (r, θ) is given by: In polar coordinates complex conjugate of (r,θ) is (r, −θ).

Question Video Representing Complex Numbers in Polar Form by

What is the conjugate of the complex number (r, θ), in polar form? Finding the conjugate of a complex number in the polar form: Let the complex number in the polar form with the coordinates (r, θ) is given by: In polar coordinates complex conjugate of (r,θ) is (r, −θ). Let $z := r \paren {\cos \theta + i \sin.

Find the polar form of the conjugate complex number of `(1i)`. YouTube

Finding the conjugate of a complex number in the polar form: The conjugate of any purely. Let the complex number in the polar form with the coordinates (r, θ) is given by: In polar coordinates complex conjugate of (r,θ) is (r, −θ). Let $z := r \paren {\cos \theta + i \sin \theta} \in \c$ be a complex number expressed.

Conjugate of a Complex Number in Polar Form YouTube

In polar coordinates complex conjugate of (r,θ) is (r, −θ). Let the complex number in the polar form with the coordinates (r, θ) is given by: Finding the conjugate of a complex number in the polar form: What is the conjugate of the complex number (r, θ), in polar form? The conjugate of any purely.

GeeklyHub Complex Numbers Definition, Polar Form, Norm, Conjugate

In polar coordinates complex conjugate of (r,θ) is (r, −θ). Finding the conjugate of a complex number in the polar form: The conjugate of any purely. Let the complex number in the polar form with the coordinates (r, θ) is given by: Let $z := r \paren {\cos \theta + i \sin \theta} \in \c$ be a complex number expressed.

How to write a complex number in polar form YouTube

What is the conjugate of the complex number (r, θ), in polar form? In polar coordinates complex conjugate of (r,θ) is (r, −θ). Finding the conjugate of a complex number in the polar form: Let $z := r \paren {\cos \theta + i \sin \theta} \in \c$ be a complex number expressed in polar form. Let the complex number in.

Polar form of complex numbers How to calculate? YouTube

In polar coordinates complex conjugate of (r,θ) is (r, −θ). Let $z := r \paren {\cos \theta + i \sin \theta} \in \c$ be a complex number expressed in polar form. Let the complex number in the polar form with the coordinates (r, θ) is given by: Finding the conjugate of a complex number in the polar form: The conjugate.

The conjugate of any purely. What is the conjugate of the complex number (r, θ), in polar form? Let $z := r \paren {\cos \theta + i \sin \theta} \in \c$ be a complex number expressed in polar form. Let the complex number in the polar form with the coordinates (r, θ) is given by: Finding the conjugate of a.

Question Video Simplifying Complex Number Expressions Using Conjugates

Let $z := r \paren {\cos \theta + i \sin \theta} \in \c$ be a complex number expressed in polar form. What is the conjugate of the complex number (r, θ), in polar form? Let the complex number in the polar form with the coordinates (r, θ) is given by: In polar coordinates complex conjugate of (r,θ) is (r, −θ)..

Complex Numbers

Let the complex number in the polar form with the coordinates (r, θ) is given by: The conjugate of any purely. Let $z := r \paren {\cos \theta + i \sin \theta} \in \c$ be a complex number expressed in polar form. What is the conjugate of the complex number (r, θ), in polar form? Finding the conjugate of a.

Convert Polar to Cartesian SammyhasHoffman

What Is The Conjugate Of The Complex Number (R, Θ), In Polar Form?

The conjugate of any purely. Finding the conjugate of a complex number in the polar form: Let the complex number in the polar form with the coordinates (r, θ) is given by: In polar coordinates complex conjugate of (r,θ) is (r, −θ).